สรุปพีทาโกรัสฉบับเข้าใจง่าย นำไปใช้ได้ทันที
ทฤษฎีพีทาโกรัส คือทฤษฎีที่สามารถนำไปใช้ในการแก้ปัญหาทางคณิตศาสตร์ และวิศวกรรมศาสตร์ได้ ซึ่งเป็นหนึ่งในบทเรียนที่น้อง ๆ จำเป็นต้องรู้ เพื่อนำไปประยุกต์ใช้ในการเรียน และการสอบเข้ามหาวิทยาลัย แต่หากน้อง ๆ คนไหนที่รู้สึกว่าเรียนในห้องยังไม่เข้าใจ หรือลืมเรื่องพีทาโกรัสไปหมดแล้ว พี่มังกี้ได้สรุปพีทาโกรัส ที่คัดเฉพาะสิ่งที่ต้องรู้เกี่ยวกับบทเรียนมาฝากกัน พร้อมยกตัวอย่างและเทคนิคการจำที่จะช่วยให้น้อง ๆ สามารถนำไปใช้ทำข้อสอบพีทาโกรัสได้ง่ายยิ่งขึ้น
ทฤษฎีบทพีทาโกรัส
สิ่งแรกที่ต้องรู้เกี่ยวกับพีทาโกรัสคงหนีไม่พ้นทฤษฎีบทพีทาโกรัส ซึ่งเป็นทฤษฎีที่กล่าวถึงความสัมพันธ์ระหว่างด้านทั้งสามของรูปสามเหลี่ยมมุมฉาก ซึ่งในทางทฤษฎีได้บอกเอาไว้ว่า
“สำหรับรูปสามเหลี่ยมมุมฉากใด ๆ พื้นที่ของรูปสี่เหลี่ยมจัตุรัสบนด้านตรงข้ามมุมฉาก เท่ากับผลรวมของพื้นที่ของรูปสี่เหลี่ยมจัตุรัสบนด้านประกอบมุมฉาก”
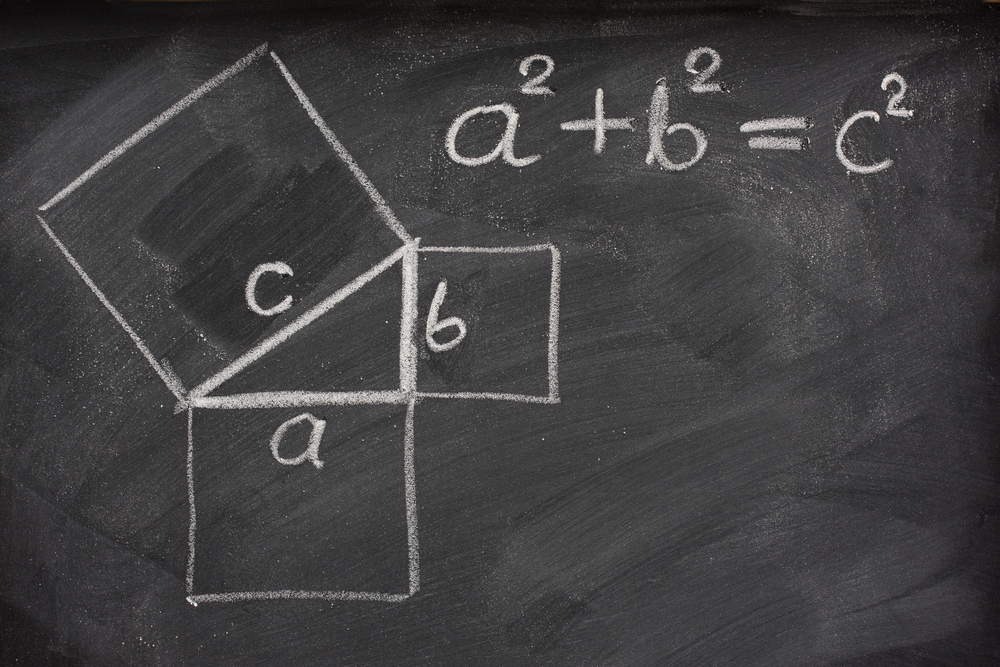
และเมื่อนำมาประกอบกับสูตรการหาพื้นที่รูปสี่เหลี่ยมจัตุรัสซึ่งก็คือ “ด้าน x ด้าน” ก็จะสามารถสรุปได้อีกอย่างหนึ่งว่า
“ด้านตรงข้ามมุมฉากกำลังสอง เท่ากับผลรวมของด้านประกอบมุมฉากกำลังสอง” นั่นเอง
สูตรพีทาโกรัส
จากทฤษฎีบทพีทาโกรัส ทำให้เราสามารถเขียนสูตรพีทาโกรัสเพื่อหาความยาวของด้านต่าง ๆ ของสามเหลี่ยมมุมฉากได้ดังนี้
“a² + b² = c² ”
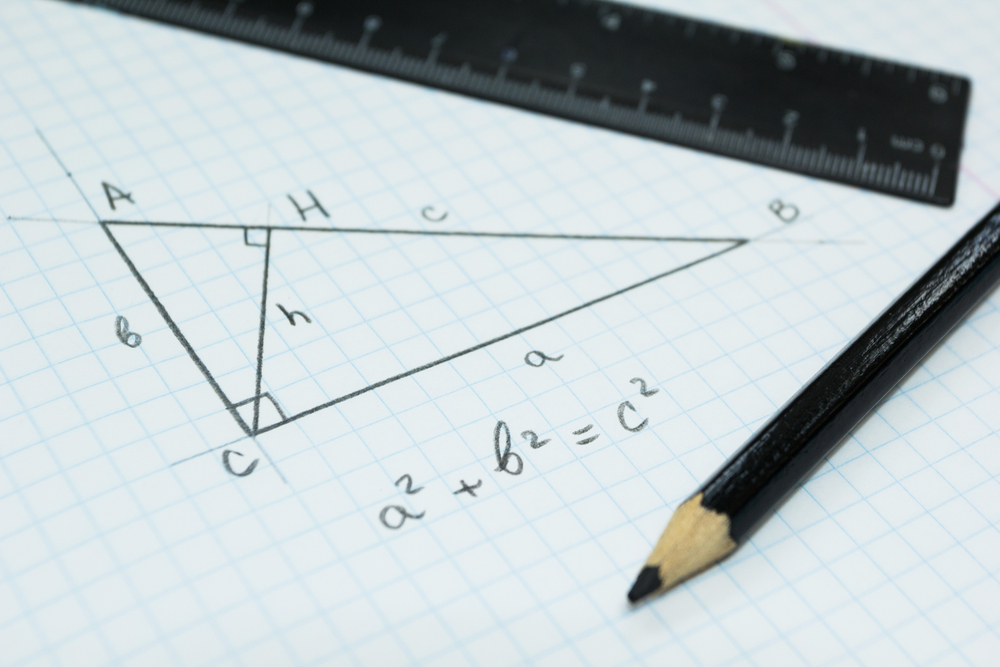
เมื่อ a แทน ความยาวตรงข้ามมุม A ซึ่งเป็นด้านประกอบมุมฉาก
b แทน ความยาวตรงข้ามมุม B ซึ่งเป็นด้านประกอบมุมฉาก
c แทน ความยาวตรงข้ามมุม C ซึ่งเป็นด้านตรงข้ามมุมฉาก เมื่อมุม C เป็นมุมฉาก
ด้าน AB เรียกว่า ด้านตรงข้ามมุมฉาก
ด้าน AC และ BC เรียกว่า ด้านประกอบมุมฉาก
จะเห็นได้ว่า หากเรามีแค่เพียงความยาวของด้านสามเหลี่ยมมุมฉากทั้ง 2 ด้าน ก็จะสามารถหาความยาวของด้านที่เหลือออกมาได้แล้ว
ตัวอย่างโจทย์พีทาโกรัส
รู้จักกับสูตรพีทาโกรัสกันไปแล้ว คราวนี้ลองมาดูตัวอย่างการนำสูตรพีทาโกรัสไปใช้ในการหาความยาวด้านในมุมฉากกันบ้าง
ตัวอย่างที่ 1 : หากมีสามเหลี่ยมมุมฉาก ที่ด้านประกอบมุมฉากมีความยาวเท่ากับ 3 เซนติเมตร และ 4 เซนติเมตร จงหาความยาวของด้านตรงข้ามมุมฉาก
วิธีทำ: ใช้สูตรพีทาโกรัสที่ว่า a² + b² = c² โดยกำหนดให้ a = 3 และ b = 4
a² + b² = c²
3² + 4² = c²
9 + 16 = c²
25 = c²
c = √25
c = 5 เซนติเมตร
ดังนั้น ความยาวด้านตรงข้ามมุมฉากของสามเหลี่ยมมุมฉากที่มีด้านประกอบมุมฉากยาว 3 เซนติเมตร และ 4 เซนติเมตรจะมีความยาวเท่ากับ 5 เซนติเมตร
ตัวอย่างที่ 2 : หากมีสามเหลี่ยมมุมฉาก ที่ด้านประกอบมุมฉากด้านหนึ่งมีความยาวเท่ากับ 15 เซนติเมตร และความยาวของด้านตรงข้ามมุมฉากเท่ากับ 25 เซนติเมตร จงหาความยาวของด้านประกอบมุมฉากที่เหลือ
วิธีทำ: ใช้สูตรพีทาโกรัสที่ว่า a² + b² = c² โดยกำหนดให้ a = 15 และ c = 25
a² + b² = c²
15² + b² = 25²
225 + b² = 625
b² = 625 - 225
b² = 400
b = √400
b = 20 เซนติเมตร
ดังนั้น ความยาวด้านประกอบมุมฉากของสามเหลี่ยมมุมฉากที่ด้านประกอบมุมฉากด้านหนึ่งมีความยาวเท่ากับ 15 เซนติเมตร และความยาวของด้านตรงข้ามมุมฉากเท่ากับ 25 เซนติเมตร จึงมีค่าเท่ากับ 20 เซนติเมตร
บทกลับทฤษฎีพีทาโกรัส
นอกจากสูตรจากทฤษฎีบทพีทาโกรัสที่ใช้กับสามเหลี่ยมมุมฉากอย่าง “เมื่อ c² = a² + b² สามเหลี่ยมที่ได้จะเป็นสามเหลี่ยมมุมฉาก” แล้ว ก็ยังมีทฤษฎีบทกลับพีทาโกรัสที่ช่วยบอกลักษณะของสามเหลี่ยมประเภทต่าง ๆ ได้ด้วยดังนี้
- เมื่อ c² > a² + b² สามเหลี่ยมที่ได้จะเป็นสามเหลี่ยมมุมป้าน
- เมื่อ c² < a² + b² สามเหลี่ยมที่ได้จะเป็นสามเหลี่ยมมุมแหลม
แชร์เลขชุดพีทาโกรัส แค่จำก็ตอบได้เลย
แน่นอนว่าการเข้าใจพื้นฐาน และการใช้สูตรพีทาโกรัสนั้นสำคัญมากสำหรับการนำไปประยุกต์ใช้ในบทเรียนต่อ ๆ ไป แต่การมีเคล็ดลับดี ๆ ก็สำคัญไม่แพ้กัน สำหรับเคล็ดลับในการทำโจทย์พีทาโกรัสให้ง่ายขึ้นก็คือ การจำเลขชุดพีทาโกรัส ที่เป็นตัวเลขความยาวด้านของสามเหลี่ยมมุมฉากที่พบได้บ่อย ๆ เหล่านี้
- 3,4,5
- 6,8,10
- 9,12,15
- 12,16,20
- 15,20,25
- 5,12,13
- 7,24,25
- 8,15,17
- 9,40,41
- 11,60,61
- 12,35,37
- 20,21,29
การจดจำเลขชุดเหล่านี้เอาไว้ จะช่วยให้น้อง ๆ สามารถหาความยาวด้านของสามเหลี่ยมมุมฉากได้อย่างรวดเร็วขึ้น ทำให้ทำข้อสอบได้อย่างราบรื่น แต่หากน้อง ๆ ม. 2 คนไหนที่เรียนพีทาโกรัสยังไม่ค่อยเข้าใจ หรือน้อง ๆ ม. 3 ที่อยากปรับพื้นฐานเรื่องพีทาโกรัสให้แม่นขึ้นก่อนสอบขึ้นชั้น ม.4 ที่ MonkeyEveryday มีคอร์ส
เรื่องพีทาโกรัส และเรื่องอื่น ๆ อีกมากมาย ที่จะช่วยสรุปเนื้อหา พร้อมพาน้อง ๆ ไปตะลุยโจทย์และฝึกฝนการใช้สูตรพีทาโกรัสให้คล่องมากยิ่งขึ้น แถมยังเลือกเรียนออนไลน์ได้ตามเวลาที่น้อง ๆ สะดวกได้เลย โดยสามารถเลือกคอร์สเรียนที่ใช่ทางเว็บไซต์ หรือจะปรึกษาพี่มังกี้ก่อน ก็ทักมาได้เลยที่
Facebook Fanpage: https://www.facebook.com/MonkeyEverydayOfficial และ เบอร์โทรศัพท์ 094-903-2323

